Aiming
Striking
Blocking
Struck
Approaching
Evading
KO
InRange
OppAiming
OppStriking
OppBlocking
OppStruck
OppApproaching
OppEvading
OppKO
OppInRange
Obligatorisk øvelse i 49253 Kunstig intelligens
Emne (22.5): Planlægning med STRIPS
Hovedopgave i 67162 Grafisk Kommunikation og Multimedier.
Udafbejdet af
(c991020) Jeppe Revall Frisvad
(c973867) Rasmus Revall Frisvad
I en uhyre simpel en-dimensional tegneserieverden betragtes en
bokser.
Ud fra et givent mål, at vinde over sin
modstander,
skal han nu planlægge sine handlinger.
Dette gør han vha. sin aktuelle
viden om den verden han befinder
sig i.
Bokseren er altså ikke alvidende, men må handle ud fra de
informationer, som han løbende kan sanse. Bokseren kan herved
på egen hånd bestemme sine handlinger, og kan derfor beskrives
som en autonom agent.
Der foregår en abstraktion fra den egentlige situation til bokserens
egen kognitive model af situationen.
Opgaven er nu at opstille slutningsregler, som fører til at bokseren
får en interessant og udfordrende opførsel ved konfrontation med
f.eks. en menneskestyret modstander.
Bokseringen opstilles som domænet, og med tilhørende mål,
slutningsregler, prædikater og operatorskemaer for konstantsymbolerne
(bokserne) kan planlægningssystemet STRIPS nu anvendes af en
computerstyret bokser.
Endvidere må bokseren altid være klar til at lægge en ny
plan, da vi arbejder i 'real-time' og en situation kan ændre sig
når som helst.
Som en mindre finesse har vi også valgt at lade bokseren kunne
lære når han har gjort noget godt.
Ved bokseringen forstås domænet.
I bokseringen findes to objekter, vi kan kalde dem
bokser A og bokser B,
også kaldet konstantsymboler.
Bokserne er autonome agenter og må have hver deres eksplicitte
repræsentation af viden om domænet - kognitive model.
Denne repræsentation har vi givet vores bokser i form af to sæt
prædikater som beskriver henholdsvis bokserens egen tilstand og
modstanderens formodede tilstand i en given situation, samt nogle
slutningsregler, som kan hjælpe bokseren fra en situation til en ny.
Disse slutningsregler betegnes som bokserens viden om domænet
(domain knowledge).
Endvidere ved bokseren selvfølgelig også hvilke
aktioner/operationer han har til rådighed.

For at kunne beskrive vores omskiftelige verden rent matematisk, anvender
vi 'situation calculus', hvor s0 betegner startsituationen, s' den
resulterende situation efter en aktion a er udført i situationen s.
En funktion do: AKTION X SITUATION -> SITUATION, er givet således at
s' = do(a,s).
Se
(2) for nærmere beskrivelse.
Prædikaterne bliver herved 'flydende' (fluents), da disse ændrer
sig med tiden. Vi arbejder i bokseverdenen med følgende 'flydende'
prædikater:
Aiming(s) - Bokseren sigter i situationen s.
Striking(s) - Bokseren slår i situationen s.
Blocking(s) - Han blokerer.
Approaching(s) - Han bevæger sig mod sin modstander.
Evading(s) - Han bevæger sig væk fra sin modstander.
InRange(s) - Modstanderen er inden for bokserens rækkevidde.
Struck(s) - Bokseren er ramt.
KO(s) - Bokseren er slået ud (Knock Out) i sitiationen s.


Til prædikaterne hører følgende aktioner:
Aim - Sigt på modstanderen.
Strike - Slå ud efter modstanderen.
Block - Bloker.
Approach - Bevæge sig mod modstanderen.
Evade - Bevæge sig væk fra modstanderen.
Med et prædikat Poss: AKTION X SITUATION, som fortæller om det
er muligt (possible) at udføre en aktion i en given situation,
kan vi opstille præbetingelsesaksiomer for aktionerne.


Da det altid er en betingelse at bokseren ikke er slået ud, vil vi
skrive
Poss(a,s) => ~KO(s)
og udelade dette i resten af præbetingelsesaksiomer og forklaringerne.
Poss(Aim,s) => ~Blocking(s) ^ ~Struck(s)
- Det er kun muligt at sigte, hvis bokseren ikke blokerer og
ikke er ramt.
Poss(Strike,s) => Aiming(s) ^ ~Blocking(s) ^ ~Struck(s)
- Det er kun muligt at slå, hvis bokseren sigter,
ikke blokerer og ikke er ramt.
Poss(Block,s) => ~Struck(s)
- Det er kun muligt at blokere, hvis bokseren ikke er ramt.
Poss(Approach,s)
- Det er altid muligt at nærme sig modstanderen.
Poss(Evade,s)
- Det er altid muligt at bevæge sig væk fra modstanderen.
Effekten af en aktion kan beskrives ved nogle effekt aksiomer:
do(Aim,s) => Aiming(s') ^ Poss(Strike,s') ^ ~Striking(s')
do(Strike,s) => ~Aiming(s') ^ Striking(s')
do(Block,s) => Blocking(s') ^ ~Aiming(s') ^ ~Striking(s') ^ ~Struck(s')
do(Approach,s) => Approaching(s') ^ ~Evading(s')
do(Evade,s) => Evading(s') ^ Approaching(s')
Betydningen skulle være nogenlunde klar, ellers henvises til senere
forklaringer, bl.a. næste afsnit (Planlægning).


Til at begynde med er ingen prædikater sande (~Aiming(s0), ~Striking(s0), etc.).
Ovenstående er hvad en bokser ved om sig selv. Skal vi nu også
bringe modstanderen ind i billede må vi tilføje endnu et
argument til prædikaterne.
Prædikaterne bliver nu af formen: OBJEKT X SITUATION, og kan derved
beskrive enhver situation i bokseringen.
En boksers viden om sit domæne kan efter ændringen af
prædikaterne beskrives ved nogle simple slutningsregler:
1. InRange(x,s) ^ ~Blocking(y,s) ^ Striking(x,s) => Struck(y,s)
2. ~InRange(x,s) v Blocking(y,s) v ~Striking(x,s) => ~Struck(y,s)
3. (l < dist) ^ (dist < u) => InRange(x,s)
4. Approaching(x,s) ^ (dist > u) => InRange(x,s')
5. Evading(x,s) ^ (dist < l) => InRange(x,s')
6. Evading(x,s) ^ InRange(x,s) => ~InRange(x,s')
7. ~Aiming(x,s) => ~Blocking(y,s)
Hvor dist er distancen fra x til modstanderen i situationen s. l og u er
nedre og øvre grænse i intervallet [l,u] hvorpå bokseren
mener at være inden for rækkevidde (InRange).
Slutningsreglerne er ikke med sikkerhed sande, 1.-6. fordi de er
afhængige af nogle værdier som bokseren
mener at kende
den korrekte værdi af. 7. fordi bokser y ikke nødvendigvis
behøver fjerne sin blokering når bokser x ikke sigter.
Vi har i løbet af dette afsnit formuleret en formel logisk model
for vores bokseverden og kan heraf danne bokserens kognitive model.

Plan:
Evade
Aim
Strike
Vi har valgt at bokseren i sin kognitive model ikke skal tage hensyn til
hvorvidt han er ramt (Struck) eller ej som præbetingelse, når han
planlægger sine handlinger.
Endvidere vil bokseren automatisk lade være med at blokerer når
det ikke længere indgår i hans plan. Så disse
præbetingelser behøver vi heller ikke tage hensyn til.
Derfor kan vi, med udgangspunkt i teorien, opstille følgende
operatorskemaer for vores bokseres aktioner:
O1: do(Aim(x),s)
P1: { }
F1: { Striking(x,s') }
A1: { Aiming(x,s') }
|
O2: do(Strike(x),s)
P2: { Aiming(x,s) }
F2: { Aiming(x,s') }
A2: { Striking(x,s') }
|
O3: do(Block(x),s)
P3 { }
F3 { Aiming(x,s'), Striking(x,s') }
A3 { Blocking(x,s'), ~Struck(x,s') }
|
O4: do(Approach(x),s)
P4 { }
F4 { Evading(x,s') }
A4 { Approaching(x,s') }
|
O5: do(Evade(x),s)
P5 { }
F5 { Approaching(x,s') }
A5 { Evading(x,s') }
|
|
For at gøre bokseren mere bevægelig har vi endvidere under
implementeringen valgt at udelade ~Struck(x,s') i A3, fordi det skal vise
sig at gøre bokseren mere bevægelig, forklaring følger
senere.

Bokseren skal nu tildeles et mål. Målet er naturligvis at
modstanderen
slås ud, uden at bokseren selv bliver slået ud.
Grunden til at vi ikke har opstillet nogen viden om hvordan en bokser
slås ud er at KO(x,s) følger umiddelbart af tilstrækkelig
mange Struck(x,s).
Der findes for bokser x derfor to mål ~Struck(x,s) og Struck(y,s),
da disse to synes at opveje hinanden, har vi fundet det rimeligt at lade
valget af mål blive foretaget alt efter bokserens temperatment.
Målet vælges altså tilfældigt, men jo mere
temperament en bokser har des større er chancen for at han
vælger målet Struck(y,s).
Med udgangspunkt i et mål valgt efter ovenstående metode kan
planlægningssystemet nu implementeres vha. operatorskemaerne og
'Styringsalgoritmen for STRIPS', se
(1),
med få variationer.


I korte træk planlægges som følger:
1. Vælg et delmål, hvis det er opfyldt i den givne situation
fortsættes med trin 7, ellers trin 2.
2. Er delmålet negeret fortsæt med trin 3, ellers trin 4.
3. Afgør om Fjernmængden for et operatorskema indeholder det
givne delmål, er dette tilfældet fortsættes med trin 5,
ellers trin 6.
4. Afgør om Addermængden for et operatorskema indeholder det
givne delmål, er dette tilfældet fortsættes med trin 5,
ellers trin 6.
5. Føj aktionen hørende til det aktuelle operatorskemaet til
planen, tilføj mængden af præbetingelser til
mængden af delmål og fortsæt med trin 7.
6. Anvend viden om domænet for at erstatte delmålet med andre
delmål, som medfører det ønskede delmål.
Hvorefter der fortsættes med trin 1. Er dette ikke muligt gør
vi ingenting ved målet.
7. Fjern det aktuelle delmål fra mængden af delmål.
8. Hvis mængden af delmål er tom afsluttes, ellers
fortsættes med trin 1.


Algoritmen er ikke perfekt i den forstand at den ikke tager højde for
at en aktion måske kan føre til mere end et delmål ad
gangen. Dette får dog kun en mindre betydning, for hvis bokseren
planlægger at udfører den samme aktion flere gange har det
reelt ingen betydning.
En ændring af algoritmen ville gøre den mere indviklet at
implementere og fordelene er ganske små, fordi der er så få
aktioner og fordi de lagte planer aldrig vil blive så indviklet, at det
har betydning.
Endvidere kan vi som angivet i lærebogen
(1) risikere at bokseren
lægger en plan som reelt ikke kan føres ud i livet, dette er
også af mindre betydning, da han derved blot kommer til at opføre
sig mere realistisk.
Da bokseren i punkt 6 anvender sin viden om domænet, vil han finde en
mere interessant opførsel når han skal opfylde målet
~Struck(x,s), hvis vi ikke medtager ~Struck(x,s') i A3.


For at undgå inkonsistente tilstande, som kan forekomme når
bokseren planlægger som han gør, vil det aldrig reelt være
muligt for bokseren at udføre noget inkonsistent.
Præbetingelserne, som er angivet i afsnittet om domænet
(Bokseringen), er lagt ind som stopklods før enhver aktion
udføres.
Dette giver endvidere den fordel at når bokseren skal udføre en
plan, vil han prøve at udføre så mange aktioner som
muligt på samme tid. Hele planen lader sig selvfølgelig ikke
udfører med det samme p.g.a. stopklodserne, men når en aktion
i planen bliver mulig, vil den straks blive udført.
Ved denne metode er bokseren, som ønsket, (næsten) altid igang
med at udføre en eller anden del af en plan, og planen kan dynamisk
ændre sig hen ad vejen, alt efter hvordan bokseren kan sanse at verden
har ændret sig.

Vi har valgt at lade bokseren sanse fire gange i sekundet. Det er måske
lige i underkanten, men bokserne er samtidigt sat noget ned i tempo for at
vi bedre kan følge med i hvad der foregår.
Ved sansning undersøger bokseren forhold med hensyn til sin modstander.
Hans interne repræsentation af sin modstander, i form af et sæt
flydende prædikater, opdateres.
Efter hver sansning ræsonerer bokseren over den nye situation.
I seks situationer har vi valgt at lade bokseren lægge en ny plan
fordi der er sket en vigtig ændring i forhold til den foregående
situation.
1. Fjerner modstanderen en blokering, har vi pludselig bedre muligheder for at
nå et mål, derfor lægges i denne situation en ny plan.
2. Sigter modstanderen på bokseren, og gjorde han det ikke i den
foregående situation, kan bokseren være i fare og vi lader
ham lægge en ny plan.
3. Er bokseren ikke længere inden for rækkevidde, men var han det
før, lader vi ham revidere sin plan.
4. Er bokseren netop færdig med et slag, lægger han en ny plan.
5. Er bokseren ramt, lægger han også en ny plan.
6. Til slut lader vi ham også lægge en ny plan, hvis der er
gået for lang tid (1,5 sek) uden noget vigtigt er hændt.
Efter bokseren har sanset lader vi ham også undersøge hvorvidt
den nye situation kan bruges til indlæring, dette er for bokser x
tilfældet når modstanderen er ramt (Struck(y,s)) eller
slået ud (KO(y,s)).
Mht. Indlæring har vi måtte begrænse os til kun at behandle
distancen hvorpå bokseren helst vil slå ud efter sin modstander.
Distancen er ganske vigtig fordi modstanderen mister mere energi, hvis
distancen er 'god'. Hvad en god distance er, må bokseren selv finde ud
af ved indlæring.
Distancen bokseren generelt går efter i løbet af en kamp vil
vise sig at have stor betydning for kampens udfald, dette grunder i at
bokserne ikke er ens hverken temperamentsmæssigt eller rent grafisk set.
Indlæringen kan beskrives matematisk. Vi introducerer først en
række variable:
HitDist(i) - Den formodede distance ved den i'te træffer.
HitCount - Det aktuelle antal træffere bokseren har haft.
NoHits - Antal træffere ved sidste indlæring.
OppEnergy - Modstanderens formodede energi.
OppStartEnergy - Modstanderens energi ved kampens start.
OppLoss - Modstanderens formodede tab siden sidste indlæring.
OppLossPrHit - Modstanderens formodede tab pr træffer.
Energy - Bokserens egen energi.
OldEnergy - Bokserens energi ved sidste indlæring.
BestDist - Bokserens yndlings distance.

Når en bokser sanser at han har ramt sin modstander husker han hvad
han mener distancen var da slaget blev udført.
I det tilfælde en bokser har haft nogle træffere i løbet
af en omgang lader vi ham lære af disse ved omgangens slutning.
Hvis OppEnergy er mindre end nul og modstanderen ikke er slået ud
må vi gå ud fra at OppEnergy, OppLoss og OppLossPrHit er forkerte.
Sker dette foretages følgende:
OppEnergy := OppEnergy + 10
OppLoss := OppLoss - OppLoss / OppLossPrHit
OppLossPrHit := OppLossPrHit - 1
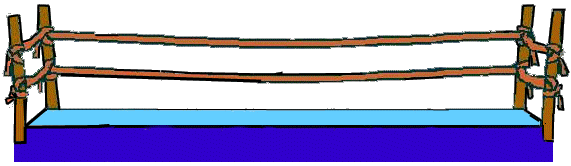
Efter ovenstående kontrol kan vi udregne den gennemsnitlige distance,
AvrHitDist, i den givne indlæringsperiode (omgangen):
AvrHitDist :=
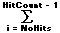
HitDist(i) / (HitCount - NoHits)


Desuden beregnes:
OppLossPrHit := (OppStartEnergy - OppEnergy) / HitCount
OppLoss := OppLossPrHit*(HitCount - NoHits) - (OldEnergy - Energy)
Er den nye beregnede OppLoss den hidtil største, har bokseren haft
den hidtil bedste omgang mod den aktuelle modstander, er det tilfældet
gemmes straks OppLoss og den nye OppLossPrHit, samt:
BestDist := AvrHitDist
Hvorved indlæringen er sket.
Endvidere udvides intervallet [l,u] hvorpå bokseren er inden for
rækkevidde (InRange) i det tilfælde at der har været nogle
træffere i yderkanten af intervallet eller ved et tilfælde
udenfor intervallet. Er dette ikke sket indsnævres intervallet en
smule for at lade interval-yderpunkterne komme tættere på
BestDist.

Efter al denne teori er vi omsider klar til
den fulde implementering af
boksespillet. Dette gøres ved en hierarkisk objekt-orienteret
opbygning af modeller,
hvori vi tilstræber at komme så tæt
på det formelle logiske sprog som muligt.
Den geometriske model omfatter form og udseende af en computerstyret figur.
Denne model er i vores program repræsenteret ved en klasse kaldet en
'TImageSprite', som indeholder en figurs position og grafiske fremstilling
(frames).
Kollisionsbestemmelse mellem figurerne hører også ind under den
geometriske model.
Den fysiske model er beskrevet ved en klasse kaldet 'TMoving', som nedarver
egenskaberne fra 'TImageSprite'.
Modellen er ganske ukompliceret, da vi befinder os i en en-dimensional
tegneserieverden.
En figur af typen 'TMoving' kan bevæges til højre eller venstre
inden for grænserne i bokseverdenen.
Biomekaniske modeller falder uden for dette spils rammer.
Men selve bokseren defineres i en ny klasse kaldet 'TBoxer', den nedarver
'TMoving' og indeholder de flydende prædikater, samt variablene
Energy og NoHits.
Dermed har vi så småt bevæget os over i
'opførselsmodellen' som er det næste trin i hierarkiet.
Til denne hører også dele af den sidste klasse kaldet
'TCPUBoxer', denne nedarver 'TBoxer' og indeholder alt den teori vi har
behandlet i de foregående afsnit, samt den kognitive model, som er
toppen af hierarkiet.
Den egentlige bokseverden, hvor bokserne initialiseres, hvor
skærmbilledet tegnes, og hvor forskellige andre småting
foregår, så som det nedtællende 'omgangsur', er helt uden
for den hierarkiske opbygningen.
Alt i alt har vi en gennemgribende forskel på bokseren kognitive model
(hans interne repræsentation af verdenen), som er givet ved
operatorskemaerne, hans planlægningsalgoritme og viden om domænet,
og den egentlig bokseverden.
Dette passer godt til den objekt-orienterede programmering og det giver en
god naturlig effekt at bokseren ikke er alvidende, når bare det ikke
overdrives.
For at bokserne handler på en interessant og udfordrende måde
kræves en del eksperimenter, især med den kognitive model og
variablenes startværdier mht. indlæringen.
Vi mener at de tidligere beskrevne operatorskemaer, planlægningen og
boksernes viden om domænet har vist sig at være bedst.
Disse kunne dog formodentlig have været lavet på mange andre
måder, men vores måde garenterer stort set konstant aktivitet
på skærmen og særdeles store udfordringer. De
computerstyrede boksere synes i hvert fald at overgå vores egne evner
som 'boksespillere'.
Det har desuden vist sig at den ene bokser har store fordele frem for den
anden. Dette har grafiske årsager, fordi
den tynde
bokser uheldigvis slår netop mellem den tykke boksers mave og hovede. Han får herved
meget sværere ved at ramme, både på tæt hold og langt
fra.
Så det har vist sig som en udfordring at få den tynde bokser til
at vinde over den tykke når de begge er computerstyret!
Her kommer indlæringen ind i billedet. Lader vi fra starten den tykke
have en BestDist som er noget mindre end den tyndes (så den tynde gerne
vil slå på lidt større afstand end den tykke). Giver vi
samtidigt den tynde evnen til indlæring, hvorimod den tykke ikke kan
lære. Da vil vi se, at hvis den tynde kan få en god omgang,
så han lærer noget, da vil han også kunne vinde hele kampen.
Det har nok været et lidt for omfattende projekt, men vi synnes at vi
har lært en hel masse, og det har været sjovt.
Vi har mange gode ideer til videreudvikling af spillet, så som
indlæring af hyppigt optrædende sekvenser af handlinger før
en god træffer, mere end en type slag og blokering, etc.
Sådanne udvidelser ville nok gøre at vi skulle til at optimere,
så spillet ville kunne køre med en acceptabel hastighed.
Spillet mangler også mange småting mht. brugervenlighed.
Vi håber opgaven dækker kravene til begge fag, og vi håber
ikke at have bevæget os for meget uden for pensum.
Det har været vældig inspirerende at kunne arbejde med det samme
projekt på to vidt forskellige måder, både mht. grafisk
kommunikation og kunstig intelligens.
Vi er glade for lærernes positive indstilling til et lidt alternativt
projekt.
Boksespillet er et fritids-projekt af ældre dato, påbegyndt for
et års tid siden. Før dette semester havde vi aldrig rigtig
haft nogen ide til hvordan bokserne skulle kunne komme til at handle
på egen hånd, det kan de nu, og det er vi glade for.
Tilmed har vi oplevet hvordan en rapport med fordel, kan udformes som en
hjemmeside.
Hvis det har interesse, kan det færdige program downloades
her.
Litteraturliste
(1) Tom Østerby
Kunstig Intelligens - metoder og systemer
Polyteknisk Forlag 1992
(2) John David Funge
AI for Games and Animation - A Cognitive Modeling Approach
A K Peters 1999






































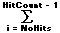 HitDist(i) / (HitCount - NoHits)
HitDist(i) / (HitCount - NoHits)

